3488. На стороне BC
треугольника ABC
как на диаметре построена окружность, пересекающая отрезок AB
в точке D
. При этом \angle ABC=\angle ACD
.
а) Докажите, что прямая CD
разбивает треугольник ABC
на два подобных треугольника.
б) Найдите отношение площадей этих подобных треугольников, если известно, что AC=15
, BC=20
.
Ответ. \frac{9}{16}
.
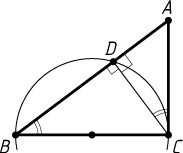
Решение. а) Точка D
лежит на окружности с диаметром BC
(рис. 1), значит, \angle ADC=\angle BDC=90^{\circ}
. Следовательно, треугольники ADC
и CDB
подобны по двум углам.
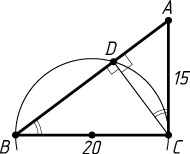
б) Треугольник ADC
подобен треугольнику CDB
с коэффициентом \frac{AC}{BC}=\frac{15}{20}=\frac{3}{4}
(рис. 2). Следовательно, их площади относятся как \left(\frac{3}{4}\right)^{2}=\frac{9}{16}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. —

