3489. Хорда AB
окружности параллельна касательной, проходящей через точку C
, лежащую на окружности.
а) Докажите, что треугольник ABC
равнобедренный.
б) Найдите радиус окружности, если известно, что расстояние между касательной и прямой AB
равно 1 и \angle ACB=150^{\circ}
.
Ответ. 2(2+\sqrt{3})
.
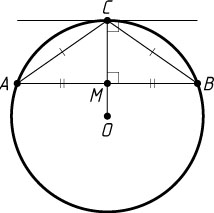
Решение. а) Пусть O
— центр окружности (рис. 1). Радиус OC
перпендикулярен данной касательной, поэтому, он перпендикулярен и параллельной ей хорде AB
, а значит, делит её пополам. Пусть M
— середина хорды AB
. Тогда CM
— высота и медиана треугольника ABC
. Следовательно, этот треугольник равнобедренный.
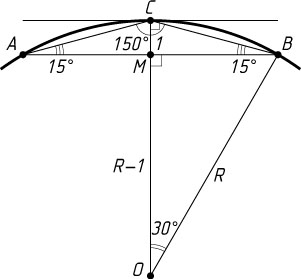
б) Из равнобедренного треугольника ABC
находим, что \angle BAC=15^{\circ}
(рис. 2). Вписанный угол BAC
равен половине соответствующего центрального угла BOC
, значит, \angle BAC=30^{\circ}
.
Пусть радиус окружности равен R
. Тогда OB=OC=R
, CM=1
, OM=OC-CM=R-1
. В прямоугольном треугольнике OMB
известно, что OM=OB\cos30^{\circ}
, или R-1=\frac{R\sqrt{3}}{2}
. Отсюда находим, что R=2(2+\sqrt{3})
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8.31, с. 76
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 8.31.1, с. 82

