3490. В полуокружности расположены две окружности, касающиеся друг друга, полуокружности и её диаметра.
а) Докажите, что периметр треугольника с вершинами в центрах окружностей и полуокружности равен диаметру полуокружности.
б) Известно, что радиус полуокружности равен 8, а радиус одной из окружностей равен 4. Найдите радиус другой.
Ответ. 2.
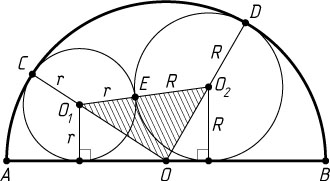
Решение. а) Пусть AB
— диаметр полуокружности, O
— её центр, O_{1}
— центр окружности радиуса r
, C
— точка её касания с полуокружностью, O_{2}
— центр окружности радиуса R
, D
— точка её касания с полуокружностью, E
— точка касания окружностей с центрами O_{1}
и O_{2}
.
Точки O
, O_{1}
и C
лежат на одной прямой, поэтому OO_{1}=OC-O_{1}C=OC-r
. Аналогично OO_{2}=OD-O_{2}D=OD-R
и O_{1}O_{2}=O_{1}E+O_{2}E=r+R
. Следовательно, периметр треугольника OO_{1}O_{2}
равен
OO_{1}+OO_{2}+O_{1}O_{2}=OC-r+OD-R+r+R=OC+OD=2OC=AB.
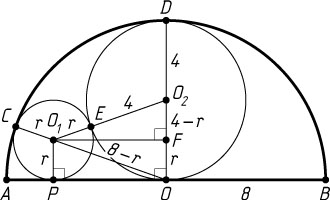
б) Пусть R=4
, OC=OD=8
. Тогда диаметр окружности с центром O_{2}
равен радиусу полуокружности, значит, OD\perp AB
, а O
— точка касания этой окружности с прямой AB
.
Пусть окружность с центром O_{1}
касается AB
в точке P
, F
— проекция точки O_{1}
на O_{2}O
. Тогда
O_{1}P=r,~O_{1}O_{2}=r+4,~O_{2}F=OO_{2}-OF=OO_{2}-O_{1}P=4-r,~OO_{1}=8-r.
Из прямоугольных треугольников OO_{1}P
и O_{1}O_{2}F
находим, что
OP^{2}=OO_{1}^{2}-O_{1}P^{2}=(8-r)^{2}-r^{2}=64-16r,
O_{1}F^{2}=O_{1}O_{2}^{2}-O_{2}F^{2}=(r+4)^{2}-(4-r)^{2}=16r,
а так как O_{1}F=OP
, то 64-16r=16r
. Следовательно, r=2
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 9.54, с. 88
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 9.54.1, с. 96

