3492. В треугольнике ABC
известно, что \angle BAC=60^{\circ}
, \angle ABC=45^{\circ}
. Продолжения высот треугольника ABC
пересекают описанную около него окружность в точках M
, N
, P
.
а) Докажите, что треугольник MNP
прямоугольный.
б) Найдите площадь треугольника MNP
, если известно, что BC=12
.
Ответ. 24\sqrt{3}
.
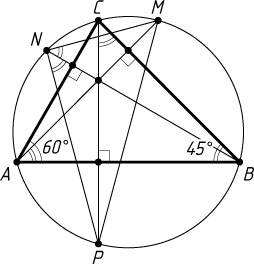
Решение. а) Пусть продолжения высот треугольника ABC
, проведённых из вершин A
, B
и C
, пересекают описанную около него окружность в точках M
, N
и P
соответственно (рис. 1). Тогда вписанные углы PNB
и PCB
опираются на одну и ту же дугу, поэтому \angle PNB=\angle PCB
. Аналогично \angle MNB=\angle MAB
, значит,
\angle PNM=\angle PNB+\angle MNB=\angle PCB+\angle MAB=
=(90^{\circ}-\angle ABC)+(90^{\circ}-\angle ABC)=90^{\circ}-45^{\circ}+90^{\circ}-45^{\circ}=90^{\circ}.
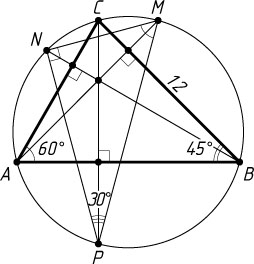
б) Аналогично получим, что \angle NMP=60^{\circ}
. Тогда \angle MPN=30^{\circ}
. Пусть R
— радиус описанной окружности треугольника ABC
(рис. 2). По теореме синусов
R=\frac{BC}{2\sin\angle BAC}=\frac{12}{2\sin60^{\circ}}=\frac{12}{\sqrt{3}}=4\sqrt{3}.
Тогда
MN=2R\sin\angle MPN=2R\sin30^{\circ}=R=4\sqrt{3},
NP=2R\sin\angle NMP=2R\sin60^{\circ}=R\sqrt{3}=12.
Следовательно,
S_{\triangle MNP}=\frac{1}{2}MN\cdot NP=\frac{1}{2}\cdot4\sqrt{3}\cdot12=24\sqrt{3}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. —

