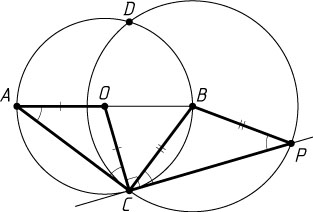
3493. Отрезок AB
— диаметр окружности с центром O
. Вторая окружность с центром в точке B
пересекается с первой окружностью в точках C
и D
. Касательная, проведённая в точке C
к первой окружности, вторично пересекает вторую окружность в точке P
.
а) Докажите, что треугольники AOC
и CBP
подобны.
б) Найдите AP
, если известно, что BC=15
и PC=24
.
Ответ. 4\sqrt{97}
.
Решение. а) Треугольники AOC
и BCP
равнобедренные. Из теоремы об угле между касательной и хордой следует, что
\angle BPC=\angle BCP=\angle CAB=\angle OAC.
Следовательно, треугольники AOC
и CBP
подобны по двум углам.
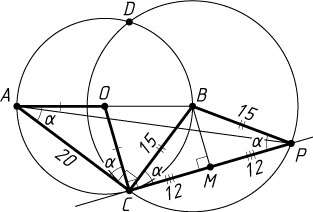
б) Пусть M
— проекция точки B
на хорду CP
второй окружности. Тогда M
— середина CP
. Обозначим \angle BAC=\angle BCM=\alpha
. Тогда \angle ACP=\angle ACB+\angle BCP=90^{\circ}+\alpha
. Из прямоугольного треугольника BMC
находим, что \cos\alpha=\frac{CM}{BC}=\frac{12}{15}=\frac{4}{5}
. Тогда \sin\alpha=\sqrt{1-\cos^{2}\alpha}=\frac{3}{5}
, \ctg\alpha=\frac{4}{3}
. Из прямоугольного треугольника ABC
находим, что AC=BC\ctg\alpha=15\cdot\frac{4}{3}=20
. По теореме косинусов
AP=\sqrt{AC^{2}+CP^{2}-2AC\cdot CP\cos(90^{\circ}+\alpha)}=\sqrt{AC^{2}+CP^{2}+2AC\cdot CP\sin\alpha}=
=\sqrt{20^{2}+24^{2}-2\cdot20\cdot24\cdot\frac{3}{5}}=4\sqrt{97}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 10.20, с. 96
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 10.21.1, с. 105

