3518. На биссектрисе внешнего угла C
треугольника ABC
взята точка M
, отличная от C
. Докажите, что MA+MB\gt CA+CB
.
Указание. Отобразите точку B
симметрично относительно прямой CM
.
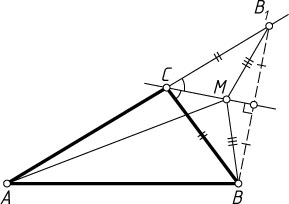
Решение. Пусть B_{1}
— точка, симметричная точке B
относительно прямой CM
. Тогда точка B_{1}
лежит на продолжении стороны AC
за точку C
, CB_{1}=CB
и MB_{1}=MB
. Поэтому
MA+MB=MA+MB_{1}\gt AB_{1}=CA+CB_{1}=CA+CB.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 17.16, с. 58
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 17.16, с. 363
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.35, с. 168
