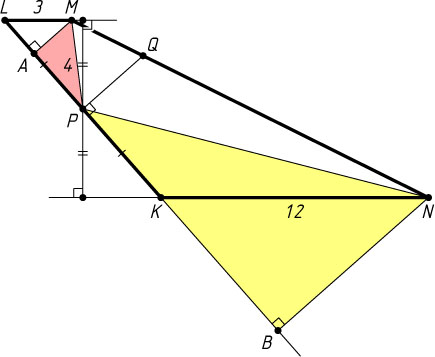
3608. В трапеции KLMN
основания KN
и LM
равны 12 и 3 соответственно. Из точки Q
, лежащей на стороне MN
, опущен перпендикуляр QP
на сторону KL
. Известно, что P
— середина стороны KL
, PM=4
и что площадь четырёхугольника PLMQ
в четыре раза меньше площади четырёхугольника PKNQ
. Найдите длину отрезка PN
.
Ответ. 16.
Указание. Если MA
и NB
— высоты треугольников LMP
и NKP
, то прямоугольные треугольники MAP
и NBP
подобны с коэффициентом \frac{1}{4}
.
Решение. Поскольку P
— середина KL
, то высоты треугольников PLM
и PKN
, опущенные из вершины P
, равны. Поэтому S_{\triangle PLM}:S_{\triangle PKN}=LM:KN=1:4
, а так как при этом S_{PLMQ}:S_{PKNQ}=1:4
, то S_{\triangle MPQ}:S_{\triangle NPQ}=1:4
. Поэтому MQ:QN=1:4
.
Пусть MA
и NB
— высоты треугольников LMP
и NKP
. Так как LP=PK
, то AM:BN=1:4
.
По теореме о пропорциональных отрезках AP:PB=MQ:QN=1:4
, поэтому прямоугольные треугольники MAP
и NBP
подобны. Следовательно, MP:PN=1:4
, откуда PN=4PM=4\cdot4=16
.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 2000 (март), вариант 2, № 4
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — 2000, вариант 2, № 4, с. 12
