3611. Окружность, проходящая через вершины B
, C
и D
параллелограмма ABCD
, касается прямой AD
и пересекает прямую AB
в точках B
и E
. Найдите длину отрезка AE
, если AD=4
и CE=5
.
Ответ. \frac{16}{5}
.
Указание. Диагонали равнобедренной трапеции BCDE
равны. Треугольник BDC
— равнобедренный. Далее примените теорему о касательной и секущей.
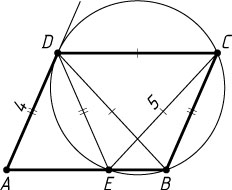
Решение. Пусть точка E
лежит между точками A
и B
. Трапеция BCDE
вписана в окружность, поэтому она равнобедренная. Значит, BD=CE=5
. Хорда BC
параллельна касательной AD
, поэтому треугольник BDC
равнобедренный (прямая, проходящая через точку D
перпендикулярно касательной AD
, проходит через центр окружности, перпендикулярна хорде BC
и делит её пополам). Следовательно, AB=CD=BD=CE=5
, и по теореме о касательной и секущей AD^{2}=AB\cdot AE
, откуда AE=\frac{AD^{2}}{AB}=\frac{16}{5}
.
Если точка не лежит между точками A
и B
, то задача не имеет решений (в этом случае, рассуждая аналогично первому случаю, получим, что AE=\frac{16}{5}\lt5
, что невозможно).
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 2000 (май), вариант 1, № 3
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 13
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.22, с. 95
