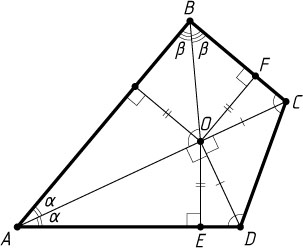
3624. Точка O
лежит на диагонали AC
выпуклого четырёхугольника ABCD
. Известно, что OC=OD
и что точка O
одинаково удалена от прямых DA
, AB
и BC
. Найдите углы четырёхугольника, если \angle AOB=110^{\circ}
и \angle COD=90^{\circ}
.
Ответ. 50^{\circ}
, 90^{\circ}
, 110^{\circ}
, 110^{\circ}
.
Указание. Опустите перпендикуляры из точки O
на прямые AD
и BC
соответственно и выразите равные углы \angle ADO
и \angle BCO
через \angle BAC=\alpha
.
Решение. Обозначим \angle BAC=\angle DAC=\alpha
, \angle ABO=\angle CBO=\beta
. Поскольку \angle BOC=70^{\circ}
— внешний угол треугольника ABO
, то \alpha+\beta=70^{\circ}
.
Пусть OE
и OF
— перпендикуляры, опущенные из точки O
на прямые AD
и BC
соответственно. Тогда точка E
лежит на отрезке AD
(основание высоты прямоугольного треугольника, проведённой из вершины прямого угла), а точка F
— на отрезке BC
(проекция основания биссектрисы BO
треугольника ABC
на его сторону BC
). Поскольку точка O
равноудалена от прямых DA
, AB
и BC
, то OF=OE
. Поэтому прямоугольные треугольники OFC
и OED
равны по гипотенузе и катету. Тогда \angle ADO=\angle BCO
, а так как
\angle ADO=90^{\circ}-\angle OAD=90^{\circ}-\alpha,
\angle BCO=90^{\circ}-\angle COF=90^{\circ}-(70^{\circ}-\angle BOF)=
=20^{\circ}+\angle BOF=20^{\circ}+(110^{\circ}-(90^{\circ}-\alpha))=40^{\circ}+\alpha,
то из уравнения 90^{\circ}-\alpha=40^{\circ}+\alpha
находим, что \alpha=25^{\circ}
. Тогда
\angle BAD=2\alpha=50^{\circ},~\angle ABC=2\beta=2(70^{\circ}-\alpha)=90^{\circ},
\angle ADC=\angle ADO+\angle ODC=(90^{\circ}-\alpha)+45^{\circ}=65^{\circ}+45^{\circ}=110^{\circ},
\angle BCD=360^{\circ}-(50^{\circ}+90^{\circ}+110^{\circ})=110^{\circ}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 2002 (март), вариант 1, № 2
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 72
