3630. Четырёхугольник ABCD
вписан в окружность. Точка X
лежит на его стороне AD
, причём BX\parallel CD
и CX\parallel BA
. Найдите BC
, если AX=\frac{3}{2}
и DX=6
.
Ответ. 3.
Указание. Треугольники ABX
, CXB
и XCD
подобны.
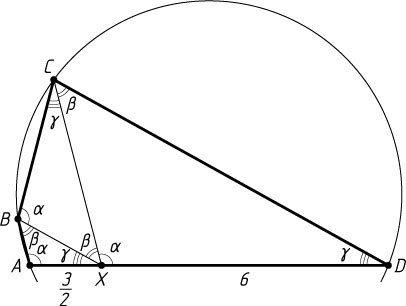
Решение. Обозначим углы при вершинах A
, B
и X
треугольника ABX
через \alpha
, \beta
и \gamma
соответственно. Поскольку CX\parallel BA
и BX\parallel CD
, то
\angle DCX=\angle BXC=\angle ABX=\beta,~\angle CDX=\angle BXA=\gamma,~\angle CXD=\angle BAX=\alpha.
Четырёхугольник ABCD
вписан в окружность, поэтому суммы его противоположных углов равны по 180^{\circ}
, значит,
\angle CBA=180^{\circ}-\angle CDA=180^{\circ}-\gamma=\alpha+\beta,
а так как \angle ABX=\beta
, то \angle CBX=\alpha
.
Таким образом, треугольники ABX
, CXB
и XCD
подобны. Перемножив почленно равенства
\frac{BC}{AX}=\frac{CX}{BX},~\frac{BC}{DX}=\frac{BX}{CX},
находим, что
BC^{2}=AX\cdot DX=\frac{3}{2}\cdot6=9,
откуда BC=3
.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 2002 (июль), вариант 1, № 4
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14.42, с. 140
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 14.42.1, с. 152
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 89
