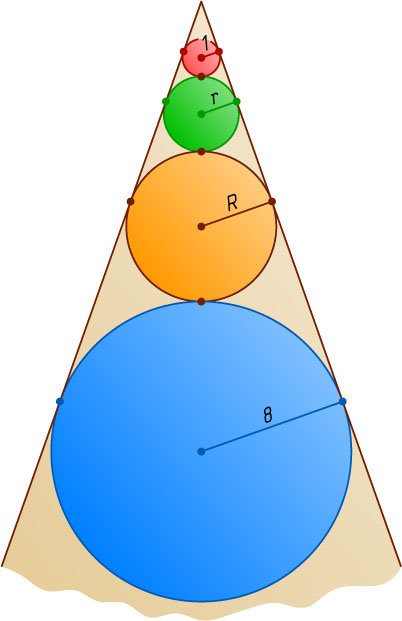
3634. В угол вписано несколько окружностей, радиусы которых возрастают. Каждая следующая окружность касается предыдущей окружности. Найдите сумму длин второй и третьей окружностей, если радиус первой равен 1, а площадь круга, ограниченного четвёртой окружностью, равна 64\pi
.
Ответ. 12\pi
.
Указание. Фигуры, состоящие из двух соседних окружностей, попарно подобны.
Решение. Поскольку площадь круга, ограниченного четвёртой окружностью, равна 64\pi
, то радиус четвёртой окружности равен 8. Пусть r
и R
— радиусы второй и третьей окружности соответственно. Заметим, что фигуры, состоящие из двух соседних окружностей, попарно подобны. Поэтому \frac{r}{1}=\frac{R}{r}=\frac{8}{R}
, откуда находим, что r=2
, R=4
. Следовательно, сумма длин второй и третьей окружностей равна 2\pi(r+R)=2\pi\cdot6=12\pi
.
Источник: Вступительный экзамен на химический факультет МГУ. — 2000 (июль), вариант 1, № 4
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 107
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.43, с. 71
