3636. В выпуклом шестиугольнике ABCDEF
все внутренние углы при вершинах равны. Известно, что AB=3
, BC=4
, CD=5
и EF=1
. Найдите длины сторон DE
и AF
.
Ответ. 6 и 8.
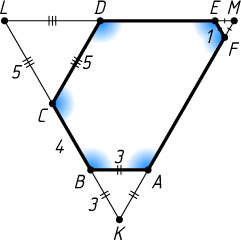
Решение. Пусть прямые AF
и BC
пересекаются в точке K
, прямые BC
и DE
— в точке L
, прямые AF
и DE
— в точке M
. Поскольку сумма внутренних углов выпуклого шестиугольника равна 180^{\circ}(6-2)=720^{\circ}
и все эти углы равны, то каждый из них равен 120^{\circ}
. Тогда треугольники AKB
, CLD
, EMF
и KLM
— равносторонние. Поэтому
AK=KB=AB=3,~CL=LD=CD=5,~EM=MF=EF=1,
KM=ML=KL=KB+BC+CL=3+4+5=12.
Тогда
DE=ML-ME-DL=12-1-5=6,
AF=KM-AK-MF=12-3-1=8.
Источник: Вступительный экзамен на химический факультет МГУ. — 2001 (май), вариант 1, № 5
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 113
