3648. В треугольник ABC
со сторонами AB=6
, BC=5
, AC=7
вписан квадрат, две вершины которого лежат на стороне AC
, одна на стороне AB
и одна на стороне BC
. Через середину D
стороны AC
и центр квадрата проведена прямая, которая пересекается с высотой BH
треугольника ABC
в точке M
. Найдите площадь треугольника DMC
.
Ответ. \frac{3\sqrt{6}}{2}
.
Указание. Докажите, что M
— середина высоты BH
.
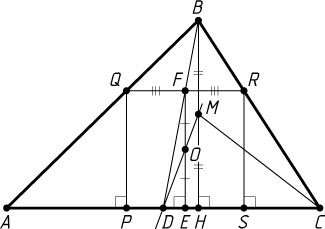
Решение. Пусть вершины P
и S
квадрата PQRS
лежат на стороне AC
(P
между A
и S
), O
— центр квадрата, F
— точка пересечения BD
и QR
. Треугольник BFR
подобен треугольнику BDC
, а треугольник BQF
— треугольнику BAD
, поэтому \frac{FR}{DC}=\frac{BF}{BD}=\frac{QF}{AD}
, а так как DC=AD
, то FR=FQ
, т. е. F
— середина QR
.
Пусть прямая FO
пересекает AC
в точке E
. Тогда FE\parallel QP\parallel BH
, а так как O
— середина FE
, то, рассуждая аналогично, докажем, что M
— середина высоты BH
.
Высота MH
треугольника DMC
вдвое меньше высоты BH
треугольника ABC
, основание DC
— вдвое меньше основания AC
, поэтому площадь треугольника DMC
в 4 раза меньше площади треугольника ABC
.
По формуле Герона находим
S_{\triangle ABC}=\sqrt{9(9-7)(9-6)(9-5)}=\sqrt{9\cdot2\cdot3\cdot4}=6\sqrt{6}.
Следовательно, S_{\triangle DMC}=\frac{1}{4}S_{\triangle ABC}=\frac{3\sqrt{6}}{2}
.
Источник: Вступительный экзамен на биологический факультет МГУ. — 2001, вариант 1, № 5
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 158
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.32, с. 114
