3654. Высота трапеции ABCD
равна 5, а основания BC
и AD
соответственно равны 3 и 5. Точка E
находится на стороне BC
, причём BE=2
, F
— середина стороны CD
, а M
— точка пересечения отрезков AE
и BF
. Найдите площадь четырёхугольника AMFD
.
Ответ. \frac{49}{4}
.
Указание. Пусть прямая BF
пересекает продолжение основания AD
в точке N
. Тогда S_{AMFD}=S_{\triangle AMN}-S_{\triangle FDN}
.
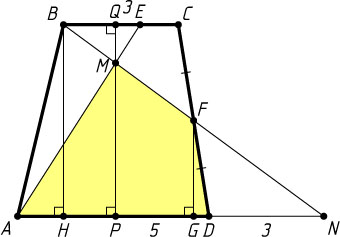
Решение. Пусть прямая BF
пересекает продолжение основания AD
в точке N
. Из равенства треугольников BCF
и NDF
следует, что DN=BC=3
. Треугольники AMN
и EMB
подобны с коэффициентом
\frac{AN}{BE}=\frac{8}{2}=4,
поэтому высота MP
треугольника AMN
в 4 раза больше высоты MQ
треугольника BME
, а так как MQ+MP=PQ=5
, то MP=\frac{4}{5}PQ=4
. Поскольку FN=BF
, то высота FG
треугольника FDN
вдвое меньше высоты BH
треугольника ABN
, поэтому
FG=\frac{1}{2}BH=\frac{5}{2}.
Следовательно,
S_{AMFD}=S_{\triangle AMN}-S_{\triangle FDN}=\frac{1}{2}\cdot AN\cdot MP-\frac{1}{2}\cdot DN\cdot FG=
=\frac{1}{2}\cdot8\cdot4-\frac{1}{2}\cdot3\cdot\frac{5}{2}=\frac{49}{4}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 2000 (май), вариант 1, № 5
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 174
