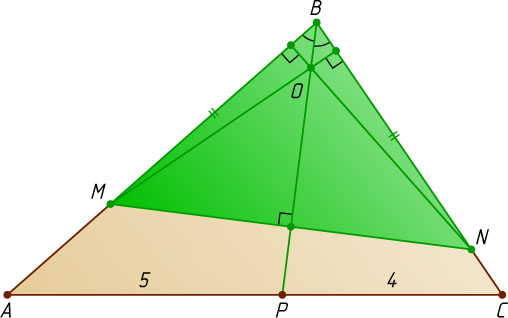
3667. В треугольнике ABC
на сторонах AB
и BC
отмечены точки M
и N
соответственно, причём BM=BN
. Через точку M
проведена прямая, перпендикулярная BC
, а через точку N
— прямая перпендикулярная AB
. Эти прямые пересекаются в точке O
. Продолжение отрезка BO
пересекает сторону AC
в точке P
и делит её на отрезки AP=6
и PC=3
. Найдите BP
, если известно, что BC=5
.
Ответ. 4\sqrt{2}
.
Решение. Высоты треугольника BMN
, проведённые из вершин M
и N
, пересекаются в точке O
, значит, его высота, проведённая из вершины B
, также проходит через точку O
, а так как треугольник BMN
равнобедренный, то луч BO
— биссектриса угла MBN
, а BP
— биссектриса треугольника ABC
. По свойству биссектрисы треугольника \frac{BC}{AB}=\frac{CP}{AP}
, откуда находим, что
AB=\frac{BC\cdot AP}{CP}=\frac{5\cdot6}{3}=10.
По формуле для биссектрисы треугольника (см. задачу 791)
BP^{2}=BC\cdot AB-CP\cdot AP=5\cdot10-3\cdot6=50-18=32.
Следовательно, BP=\sqrt{32}=4\sqrt{2}
.
Источник: Вступительный экзамен на географический факультет МГУ. — 2000 (май), вариант 2, № 4
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 207
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.20, с. 40
