3678. На катете AC
прямоугольного треугольника ABC
как на диаметре построена окружность. Она пересекает сторону AB
в точке E
. На стороне BC
взята точка G
так, что отрезок AG
пересекает окружность в точке F
, причём отрезки EF
и AC
параллельны, BG=2CG
и AC=2\sqrt{3}
. Найдите GF
.
Ответ. 1.
Указание. Треугольники ABC
и GAC
подобны по двум углам.
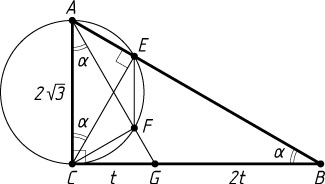
Решение. Пусть CG=t
, \angle CAG=\alpha
. Тогда BC=3t
, а так как CE
— высота прямоугольного треугольника ABC
, проведённая из вершины прямого угла, то \angle ABC=\angle ACE
. Поскольку трапеция AEFC
вписана в окружность, то она равнобедренная, поэтому \angle ACE=\angle CAG=\alpha
. Значит, \angle ABC=\angle CAG=\alpha
. Следовательно, прямоугольные треугольники ABC
и GAC
подобны по двум углам.
Из равенства \frac{CG}{AC}=\frac{AC}{BC}
следует, что AC^{2}=CG\cdot BC
, или 12=3t^{2}
, откуда t=2
.
Из прямоугольного треугольника ACG
находим, что
\tg\alpha=\frac{CG}{AC}=\frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}},
поэтому \alpha=30^{\circ}
. Тогда AG=2CG=4
.
По теореме о касательной и секущей GF\cdot AG=CG^{2}
, или 4FG=4
. Следовательно, FG=1
.
