3684. Определите угол A
между сторонами 2 и 4, если медиана, проведённая из вершины A
, равна \sqrt{7}
.
Ответ. 60^{\circ}
.
Указание. На продолжении медианы AM
данного треугольника отложите отрезок MD
, равный отрезку AM
.
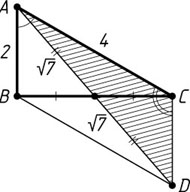
Решение. На продолжении медианы AM
данного треугольника ABC
со сторонами AB=2
и AC=4
отложим отрезок MD
, равный отрезку AM
. Тогда четырёхугольник ABDC
— параллелограмм, поэтому CD=AB=2
. Применяя теорему косинусов, из треугольника ACD
находим, что
\cos\angle ACD=\frac{AC^{2}+CD^{2}-AD^{2}}{2\cdot AC\cdot CD}=\frac{16+4-4\cdot7}{2\cdot4\cdot2}=-\frac{1}{2},
поэтому \angle ACD=120^{\circ}
. Следовательно,
\angle BAC=180^{\circ}-\angle ACD=180^{\circ}-120^{\circ}=60^{\circ}.
Источник: Вступительный экзамен на социологический факультет МГУ. — 2002 (май), вариант 1, № 3
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 267
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 2.8, с. 17
