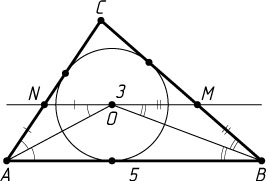
3686. Через центр окружности, вписанной в треугольник ABC
, провели прямую MN
параллельно основанию AB
(M
лежит на BC
, N
— на AC
). Найдите периметр четырёхугольника ABMN
, если известно, что AB=5
, MN=3
.
Ответ. 11.
Указание. Пусть O
— центр окружности, вписанной в треугольник ABC
. Докажите, что AN=ON
и BM=OM
.
Решение. Пусть O
— центр окружности, вписанной в треугольник ABC
. Тогда AO
— биссектриса угла CAB
. Поэтому
\angle NOA=\angle BAO=\angle NAO.
Значит, треугольник ANO
равнобедренный, AN=ON
. Аналогично BM=OM
. Следовательно,
AB+NM+AN+MB=AB+MN+NO+OM+AB+MN+MN=
=5+3+3=11.
Источник: Вступительный экзамен на филологический факультет МГУ. — 2000, вариант 1, № 2
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 273
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8.33, с. 76
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 8.33.1, с. 83
