3713. Две окружности радиусов \sqrt{19}
и \sqrt{76}
, касающиеся друг друга внешним образом, вписаны в полуокружность (т. е. каждая из окружностей касается этой полуокружности и её диаметра). Найдите радиус полуокружности.
Ответ. 4\sqrt{19}
.
Указание. Линия центров касающихся окружностей проходит через точку их касания. Составьте уравнение относительно искомого радиуса.
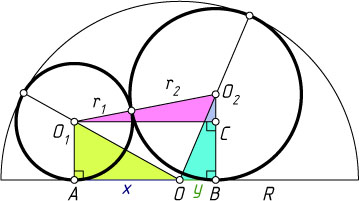
Решение. Пусть O
, O_{1}
и O_{2}
— центры полуокружности и окружностей, радиусы которых обозначим через соответственно R
, r_{1}
и r_{2}
. Пусть A
и B
— точки касания соответствующих окружностей с диаметром полуокружности, C
— проекция точки O_{1}
на O_{2}B
. Поскольку r_{1}=\sqrt{19}
, а r_{2}=2\sqrt{19}
, то r_{2}=2r_{1}
. Обозначим r_{1}=r
. Тогда r_{2}=2r
, O_{1}O_{2}=r_{1}+r_{2}=3r
, O_{2}C=2r-r=r
.
Из прямоугольного треугольника O_{1}CO_{2}
по теореме Пифагора находим, что
O_{1}C=\sqrt{O_{1}O_{2}^{2}-O_{2}C^{2}}=\sqrt{9r^{2}-r^{2}}=2r\sqrt{2}.
Обозначим AO=x
, BO=y
. Поскольку OO_{1}=R-r
и OO_{2}=R-2r
, то из прямоугольных треугольников OAO_{1}
и OBO_{2}
получаем, что
(R-r)^{2}=r^{2}+x^{2}~\mbox{и}~(R-2r)^{2}=4r^{2}+y^{2},
откуда x^{2}=(R-r)^{2}-r^{2}
и y^{2}=(R-2r)^{2}-4r^{2}
, а так как x+y=AB=2r\sqrt{2}
, то получаем уравнение
\sqrt{R^{2}-2Rr}+\sqrt{R^{2}-4Rr}=2r\sqrt{2}.
Сделав замену t=\frac{R}{r}
, получим иррациональное уравнение
\sqrt{t^{2}-2t}=2\sqrt{2}-\sqrt{t^{2}-4t}.
После возведения обеих частей в квадрат получим уравнение 2\sqrt{2}\sqrt{t^{2}-4t}=4-t
, откуда следует, что t=4
.
Таким образом, R=4r=4\sqrt{19}
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1999 (май), вариант 1, № 8
Источник: Математика. Задачи вступительных экзаменов с ответами и решениями / Сост. Е. А. Григорьев. — М.: УНЦ ДО, 2004. — с. 33
