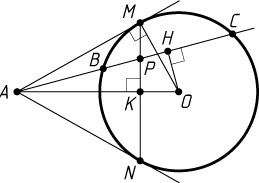
3807. Из точки A
проведены к окружности две касательные (M
и N
— точки касания) и секущая, пересекающая эту окружность в точках B
и C
, а хорду MN
— в точке P
, AB:BC=2:3
. Найдите AP:PC
.
Ответ. 4:3
.
Указание. Пусть O
— центр окружности, прямая AO
пересекает хорду MN
в точке K
, H
— проекция точки O
на хорду BC
. Тогда
AB\cdot AC=AM^{2}=AO\cdot AK=AH\cdot AP.
Решение. Пусть O
— центр окружности, а прямая AO
пересекает хорду MN
в точке K
. Тогда AK\perp MN
. Из прямоугольного треугольника AOM
находим, что AM^{2}=AO\cdot AK
.
Пусть H
— проекция точки O
на хорду BC
. Тогда H
— середина BC
. Прямоугольные треугольники AKP
и AHO
подобны по двум углам, поэтому \frac{AK}{AP}=\frac{AH}{AO}
, откуда AO\cdot AK=AH\cdot AP
.
По теореме о касательной и секущей AM^{2}=AB\cdot AC
.
Из полученных равенств следует, что
AB\cdot AC=AM^{2}=AO\cdot AK=AH\cdot AP.
Обозначим AB=2x
, BC=3x
. Тогда
AC=AB+BC=5x,~AH=\frac{1}{2}\cdot(AB+AC)=\frac{7}{2}x.
Из равенства AB\cdot AC=AH\cdot AP
находим, что
AP=\frac{AB\cdot AC}{AH}=\frac{2x\cdot5x}{\frac{7}{2}x}=\frac{20x}{7}.
Тогда PC=AC-AP=5x-\frac{20x}{7}=\frac{15x}{7}
.
Следовательно,
\frac{AP}{PC}=\frac{\frac{20x}{7}}{\frac{15x}{7}}=\frac{4}{3}.
Источник: Вступительный экзамен на физический факультет МГУ. — 2000 (март), вариант 1, № 8
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.23, с. 47
