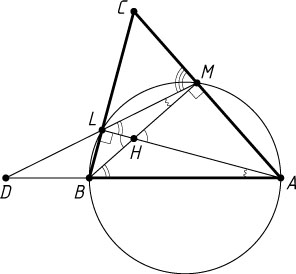
3842. В треугольнике ABC
провели высоты AL
и BM
, причём точки L
и M
оказались лежащими на сторонах BC
и AC
соответственно. Затем провели прямую LM
до пересечения с продолжением стороны AB
. Какое наибольшее количество пар подобных треугольников можно насчитать на этом чертеже, если на нём не образовалось ни одной пары равных треугольников?
Ответ. 10.
Указание. Точки A
, B
, M
и L
лежат на одной окружности.
Решение. Прямоугольные треугольники CAL
и CBM
подобны по двум углам (угол C
— общий).
Пусть H
— точка пересечения высот данного треугольника. Прямоугольные треугольники AMH
и BLH
подобны по двум углам (углы AHM
и BHL
— вертикальные).
Прямоугольные треугольники AMH
и ALC
подобны по двум углам (угол A
— общий).
Прямоугольные треугольники BLH
и BMC
подобны по двум углам (угол B
— общий).
Следовательно, подобны прямоугольные треугольники AMH
и BMC
, а также прямоугольные треугольники BLH
и ALC
.
Из точек M
и L
отрезок AB
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AB
. Тогда \angle BML=\angle BAL
как вписанные углы, опирающиеся на одну дугу. Значит, треугольники MHL
и AHB
подобны по двум углам.
Поскольку сумма противоположных углов вписанного четырёхугольника равна 180^{\circ}
, то
\angle MAB=180^{\circ}-\angle MLB=\angle CLM,
значит, треугольники CLM
и CAB
подобны по двум углам (угол C
— общий).
Пусть прямые AB
и ML
пересекаются в точке D
. Аналогично предыдущему докажем, что треугольники DBL
и DMA
подобны по двум углам (угол D
— общий).
Наконец, из равенства \angle BML=\angle BAL
следует, что подобны треугольники DBM
и DLA
.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1999 (тестирование), вариант 7, № 8
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.8, с. 122
