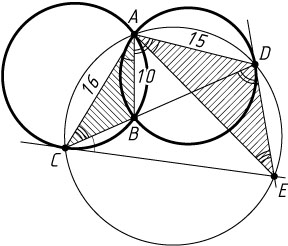
3847. Две окружности пересекаются в точках A
и B
. Через точку B
проведена прямая, пересекающая окружности в точках C
и D
, лежащих по разные стороны от прямой AB
. Касательные к этим окружностям в точках C
и D
пересекаются в точке E
. Найдите AE
, если AB=10
, AC=16
, AD=15
.
Ответ. 24.
Указание. Докажите, что около четырёхугольника ABCD
можно описать окружность, а также, что треугольники ABC
и ADE
подобны.
Решение. Из теоремы об угле между касательной и хордой следует, что \angle BAC=\angle ECD
и \angle BAD=\angle EDC
. Поскольку луч AB
лежит между сторонами угла CAD
, то
\angle CAD=\angle BAC+\angle BAD=\angle ECD+\angle EDC=180^{\circ}-\angle CED.
Следовательно, около четырёхугольника ADEC
можно описать окружность.
Докажем подобие треугольников ABC
и ADE
. Действительно, так как четырёхугольник ABCD
— вписанный, то \angle BAC=\angle ECD=\angle EAD
как вписанные углы, опирающиеся на одну дугу. Аналогично, \angle ACB=\angle AED
. Следовательно, треугольники ABC
и ADE
подобны по двум углам.
Тогда \frac{AE}{AC}=\frac{AD}{AB}
, откуда находим, что
AE=\frac{AD\cdot AC}{AB}=\frac{15\cdot16}{10}=24.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1999 (май), вариант 1, № 4
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 13.43, с. 130
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 13.43.1, с. 141
