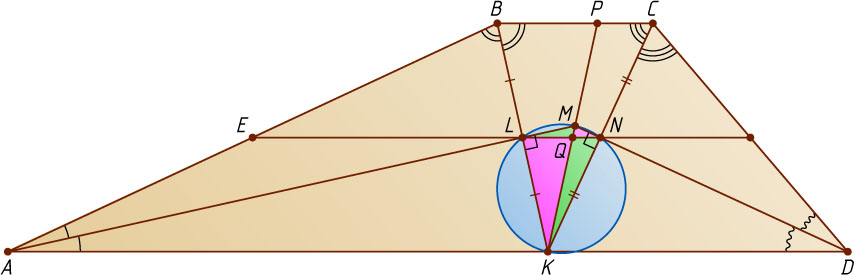
3851. В трапеции ABCD
с боковыми сторонами AB=9
и CD=5
биссектриса угла D
пересекает биссектрисы углов A
и C
в точках M
и N
соответственно, а биссектриса угла B
пересекает те же две биссектрисы в точках L
и K
, причём точка K
лежит на основании AD
.
а) В каком отношении прямая LN
делит сторону AB
, а прямая MK
— сторону BC
?
б) Найдите отношение MN:KL
, если LM:KN=3:7
.
Ответ. а) 1:1
; 5:9
; б) 5:21
.
Решение. Поскольку BK
— биссектриса угла ABC
, а прямые BC
и AD
параллельны, то \angle ABK=\angle KBC=\angle AKB
, поэтому треугольник ABK
— равнобедренный. Значит, AK=AB=9
и биссектриса AL
этого треугольника является его медианой и высотой, т. е. BL=KL
и AL\perp BK
. Аналогично докажем, что DK=CD=5
, CN=KN
и DN\perp CK
.
Таким образом, LN
— средняя линия треугольника BKC
, поэтому прямая LN
параллельна основаниям трапеции, а точка E
пересечения прямых LN
и AB
— середина стороны AB
. Следовательно, AE:BE=1:1
.
Пусть прямая MK
пересекается с прямыми BC
и LN
в точках P
и Q
соответственно. Поскольку LN\parallel BC
и LN\parallel AD
, то CP:PB=NQ:QL=DK:AK=5:9
.
Отрезок MK
виден из точек L
и N
под прямым углом, значит точки L
и N
лежат на окружности с диаметром MK
, поэтому треугольники MQL
и NQK
подобны по двум углам. Тогда MQ:NQ=LM:KN=\frac{3}{7}
, откуда находим, что MQ=NQ\cdot\frac{LM}{KN}=\frac{3}{7}\cdot NQ
.
Из подобия треугольников MQN
и LQK
следует, что
\frac{MN}{KL}=\frac{MQ}{QL}=\frac{\frac{3}{7}NQ}{QL}=\frac{3}{7}\cdot\frac{NQ}{QL}=\frac{3}{7}\cdot\frac{5}{9}=\frac{5}{21}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1999 (июль), вариант 1, № 4
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.22, с. 47
