3856. Сторона BC
треугольника ABC
равна 12. Около треугольника описана окружность радиуса 10. Найдите стороны AB
и AC
треугольника, если известно, что радиус OA
окружности делит сторону BC
на два равных отрезка.
Ответ. 2\sqrt{10}
.
Указание. Радиус окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
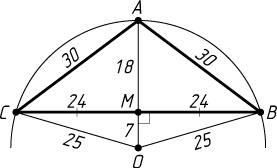
Решение. Пусть M
— середина хорды BC
. Поскольку BC=12
, то BC
— не диаметр окружности. Известно, что радиус окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде, значит, OM
— высота равнобедренного треугольника BOC
.
Высота AM
треугольника ABC
является его медианой, поэтому треугольник ABC
— равнобедренный.
Из прямоугольного треугольника OMB
находим, что
OM=\sqrt{OB^{2}-BM^{2}}=\sqrt{100-36}=\sqrt{64}=8.
Поэтому AM=OA-OM=10-8=2
. Следовательно,
AC=BC=\sqrt{BM^{2}+AM^{2}}=\sqrt{36+4}=\sqrt{40}=2\sqrt{10}.
Источник: Вступительный экзамен на филологический факультет МГУ. — 1998, вариант 1, № 2
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.41.1, с. 117
