3878. В окружность радиуса \sqrt{7}
вписана трапеция с меньшим основанием 4. Через точку на этой окружности, касательная в которой параллельна одной из боковых сторон трапеции, проведена параллельная основаниям трапеции хорда окружности длины 5. Найдите длину диагонали трапеции и площадь трапеции.
Ответ. 5; \frac{975\sqrt{3}}{196}
.
Указание. Докажите, что хорда из условия задачи и диагональ трапеции стягивают равные дуги и, следовательно, равны. С помощью теорем синусов и косинусов составьте тригонометрическое уравнение относительно угла между диагональю и основанием трапеции.
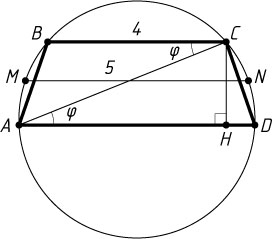
Решение. Пусть ABCD
— данная трапеция с меньшим основанием BC=4
, M
— данная точка на меньшей дуге AB
, причём касательная к описанной окружности радиуса R=\sqrt{7}
, проведённая в этой точке, параллельна боковой стороне AB
. Ясно, что M
— середина дуги AB
.
Вписанная в окружность трапеция — равнобедренная. Прямая, проходящая через точку M
параллельно основаниям трапеции, пересекает меньшую дугу CD
в её середине N
.
Дуги, заключённые между параллельными хордами, равны, поэтому меньшая дуга CD
равна меньшей дуге AB
, значит, равны и половины этих дуг, т. е. меньшие дуги AM
и CN
. Отсюда следует, что хорды AC
и MN
равны, так как они стягивают равные дуги AMBC
и MBCN
. Таким образом, диагональ AC
равна 5.
Обозначим \angle ACB=\angle CAD=\varphi
. Тогда AB=CD=2R\sin\varphi=2\sqrt{7}\sin\varphi
. По теореме косинусов
AB^{2}=BC^{2}+CA^{2}-2\cdot BC\cdot CA\cdot\cos\angle ACB,~\mbox{или}~28\sin^{2}\varphi=16+25-2\cdot4\cdot5\cdot\cos\varphi.
Из этого уравнения находим, что \cos\varphi=\frac{13}{14}
или \cos\varphi=\frac{1}{2}
.
Рассмотрим первый случай.
Пусть CH
— высота трапеции. Из прямоугольного треугольника AHC
находим, что
AH=AC\cdot\cos\varphi=5\cdot\frac{13}{14}=\frac{65}{14},~CH=AC\cdot\sin\varphi=5\cdot\frac{3\sqrt{3}}{14}=\frac{15\sqrt{3}}{14}.
Поскольку трапеция — равнобедренная, то отрезок AH
(проекция диагонали трапеции на большее основание) равен средней линии трапеции. Следовательно,
S_{ABCD}=AH\cdot CH=\frac{65}{14}\cdot\frac{15\sqrt{3}}{14}=\frac{975\sqrt{3}}{196}.
Во втором случае AH=5\cdot\frac{1}{2}=\frac{5}{2}\lt4
, что невозможно, так как средняя линия не может быть меньше, чем меньшее основание трапеции.
Источник: Вступительный экзамен на факультет психологии МГУ. — 2003, вариант 1, № 4
Источник: Вступительные экзамены и олимпиады по математике 2003—2005 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2006. — с. 159
