3909. В треугольнике ABC
выполнено соотношение между сторонами \frac{AC-AB}{BC+AB}=\frac{AB-BC}{AC+AB}
. Найдите радиус описанной окружности, если расстояние от её центра до точки пересечения медиан равно d
, а длина стороны AB
равна c
.
Ответ. \sqrt{d^{2}+\frac{c^{2}}{3}}
.
Указание. Пусть AC=b
, AB=c
, BC=a
. Из условия задачи следует, что a^{2}+b^{2}=2c^{2}
. Пусть O
— центр окружности радиуса, описанной около треугольника ABC
, M
— точка пересечения медиан. Вычислите скалярный квадрат вектора
\overrightarrow{OM}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}).
Решение. Обозначим AC=b
, AB=c
, BC=a
.
Из условия задачи следует, что
\frac{AC-AB}{BC+AB}=\frac{AB-BC}{AC+AB}=\frac{b-c}{a+c}=\frac{c-a}{b+c}~\Rightarrow
\Rightarrow~b^{2}-c^{2}=c^{2}-a^{2}~\Rightarrow~a^{2}+b^{2}=2c^{2}.
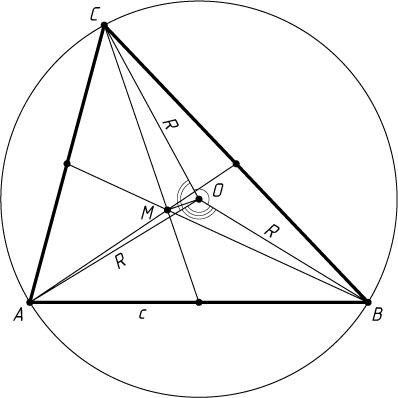
Пусть O
— центр окружности радиуса R
, описанной около треугольника ABC
, M
— точка пересечения медиан. Тогда
\overrightarrow{OM}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}).
Обозначим
\angle AOB=2\gamma,~\angle AOC=2\beta,~\angle BOC=2\alpha.
(половина каждого из этих углов равна соответствующему углу треугольника ABC
или дополняет его до 180^{\circ}
). Тогда
d^{2}=\overrightarrow{OM}^{2}=\frac{1}{9}(\overrightarrow{OA}^{2}+\overrightarrow{OB}^{2}+\overrightarrow{OC}^{2}+2\overrightarrow{OA}\cdot\overrightarrow{OB}+2\overrightarrow{OA}\cdot\overrightarrow{OC}+2\overrightarrow{OB}\cdot\overrightarrow{OC})=
=\frac{1}{9}(R^{2}+R^{2}+R^{2}+2R\cdot R\cdot\cos2\gamma+2R\cdot R\cdot\cos2\beta+2R\cdot R\cdot\cos2\alpha)=
=\frac{1}{9}R^{2}(3+2(\cos2\gamma+\cos2\beta+\cos2\alpha))=
=\frac{1}{9}R^{2}(3+2(1-2\sin^{2}\gamma+1-2\sin^{2}\beta+1-2\sin^{2}\alpha))=
=\frac{1}{9}R^{2}(9-4(\sin^{2}\gamma+\sin^{2}\beta+\sin^{2}\alpha))=
=\frac{1}{9}R^{2}\left(9-4\left(\left(\frac{c}{2R}\right)^{2}+\left(\frac{b}{2R}\right)^{2}+\left(\frac{a}{2R}\right)^{2}\right)\right)=
=R^{2}-\frac{1}{9}\cdot4\cdot\frac{1}{4}(a^{2}+b^{2}+c^{2})=R^{2}-\frac{1}{9}\cdot3c^{2}=R^{2}-\frac{c^{2}}{3}.
Следовательно, R^{2}=d^{2}+\frac{c^{2}}{3}
.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1998 (отделение экономики), вариант 2, № 6
