3910. Две окружности радиусов 4 и 3 касаются друг друга внешним образом. К этим окружностям проведены общие внешние касательные PQ
и RS
таким образом, что точки P
и S
принадлежат окружности большего радиуса, а точки Q
и R
принадлежат окружности меньшего радиуса. Найдите радиус окружности, касающейся отрезков RS
, SP
и PQ
.
Ответ. \frac{24}{7}
.
Указание. Из теоремы об угле между касательной и хордой следует, что точка касания окружностей есть точка пересечения биссектрис данного четырёхугольника, т. е. центр его вписанной окружности. Остаётся найти расстояние от этой точки до общей внешней касательной данных окружностей.
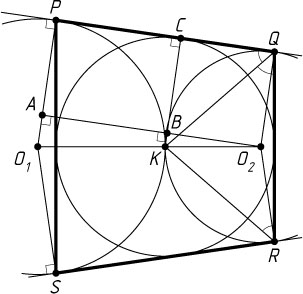
Решение. Пусть окружность с центром O_{1}
радиуса 4 и окружность с центром O_{2}
радиуса 3 касаются внешним образом в точке K
. Тогда K
— середина дуг QKR
и PQS
этих окружностей.
Из теоремы об угле между касательной и хордой следует, что
\angle PQK=\angle QRK=\angle RQK.
Значит, QK
— биссектриса угла PQR
четырёхугольника PQRS
. Аналогично докажем, что PK
, RK
и SK
— биссектрисы остальных углов четырёхугольника PQRS
.
Таким образом, биссектрисы углов данного четырёхугольника пересекаются в точке K
, поэтому в четырёхугольник PQRS
можно вписать окружность, а точка K
— центр этой окружности.
Пусть C
— проекция точки K
на сторону PQ
. Тогда KC
— радиус вписанной окружности четырёхугольника PQRS
.
Из вершины O_{2}
прямоугольной трапеции O_{2}QPO_{1}
опустим перпендикуляр O_{2}A
на основание O_{1}P
. Пусть отрезки O_{2}A
и KC
пересекаются в точке B
. Тогда PA=BC=O_{2}Q=3
.
Из подобия треугольников O_{2}BK
и O_{2}AO_{1}
находим, что
KB=O_{1}A\cdot\frac{O_{2}K}{O_{2}O_{1}}=(O_{1}P-AP)\cdot\frac{O_{2}K}{O_{2}K+KO_{1}}=(4-3)\cdot\frac{3}{3+4}=\frac{3}{7}.
Следовательно,
KC=KB+BC=\frac{3}{7}+3=\frac{24}{7}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1998 (отделение менеджмента), вариант 1, № 5
