3918. На стороне PQ
треугольника PQR
взята точка N
, а на стороне PR
— точка L
, причём NQ=LR
. Точка пересечения отрезков QL
и NR
делит отрезок QL
в отношении m:n
, считая от точки Q
. Найдите отношение PN:PR
.
Ответ. \frac{n}{m}
.
Указание. Пусть отрезки QL
и NR
пересекаются в точке A
. Через точку Q
проведите прямую, параллельную PR
. Если эта прямая пересекается с прямой NR
в точке B
, то треугольник BAQ
подобен треугольнику RAL
, а треугольник BNQ
— треугольнику PNR
.
Решение. Пусть отрезки QL
и NR
пересекаются в точке A
. Обозначим NQ=LR=a
.
Через точку Q
проведём прямую, параллельную PR
. Пусть эта прямая пересекается с прямой NR
в точке B
. Из подобия треугольников BAQ
и RAL
следует, что BQ=LR\cdot\frac{AQ}{AL}=a\cdot\frac{m}{n}
. Из подобия треугольников BNQ
и RNP
находим, что
\frac{PN}{PR}=\frac{NQ}{BQ}=\frac{a}{a\cdot\frac{m}{n}}=\frac{n}{m}.
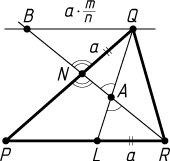
Источник: Вступительный экзамен на физический факультет МГУ. — 1997 (март), вариант 1, № 6
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.11, с. 46
