3924. В трапеции ABCD
известно, что BC\parallel AD
, \angle ABC=90^{\circ}
. Прямая, перпендикулярная стороне CD
, пересекает сторону AB
в точке M
, а сторону CD
— в точке N
. Известно также, что MC=a
, BN=b
, а расстояние от точки D
до прямой MC
равно c
. Найдите расстояние от точки A
до прямой BN
.
Ответ. \frac{bc}{a}
.
Решение. Из точек B
и N
отрезок MC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром MC
. Вписанные в эту окружность углы MBN
и MCN
опираются на одну и ту же дугу. Следовательно,
\angle ABN=\angle MBN=\angle MCN=\angle MCD.
Из точек A
и N
отрезок MD
виден под прямым углом, значит, эти точки лежат на окружности с диаметром MD
. Вписанные в эту окружность углы MDN
и MAN
опираются на одну и ту же дугу. Следовательно,
\angle BAN=\angle MAN=\angle MDN=\angle MDC.
Из доказанного следует, что треугольники ANB
и DMC
подобны по двум углам. Значит, отношение их соответствующих высот AQ
и DP
равно отношению оснований, т. е.
\frac{AQ}{DP}=\frac{BN}{MC},~\mbox{или}~\frac{AQ}{c}=\frac{b}{a}.
Следовательно, AQ=\frac{bc}{a}
.
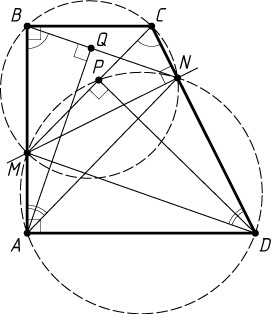
Источник: Вступительный экзамен на физический факультет МГУ. — 1997 (июль), вариант 1, № 8
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.31, с. 114
