3932. В треугольнике ABC
угол C
равен 60^{\circ}
, а биссектриса угла C
равна 5\sqrt{3}
. Длины сторон AC
и BC
относятся как 5:2
соответственно. Найдите тангенс угла A
и сторону BC
.
Ответ. \frac{\sqrt{3}}{4}
; 7.
Указание. Пусть CD
— биссектриса данного треугольника. Обозначим BC=2t
, AC=5t
. Найдите t
из уравнения
S_{\triangle ABC}=S_{\triangle BCD}+S_{\triangle ACD}
Решение. Пусть CD=5\sqrt{3}
— биссектриса данного треугольника. Обозначим BC=2t
, AC=5t
. Тогда
S_{\triangle ABC}=\frac{1}{2}\cdot BC\cdot AC\sin60^{\circ}=\frac{5}{2}t^{2}\sqrt{3},
S_{\triangle ABC}=S_{\triangle BCD}+S_{\triangle ACD}=\frac{1}{2}\cdot BC\cdot CD\sin30^{\circ}+\frac{1}{2}\cdot AC\cdot CD\sin30^{\circ}=
=\frac{1}{2}\cdot2t\cdot5\sqrt{3}\cdot\frac{1}{2}+\frac{1}{2}\cdot5t\cdot5\sqrt{3}\cdot\frac{1}{2}=\frac{1}{2}\cdot7t\cdot5\sqrt{3}\cdot\frac{1}{2}=\frac{35}{4}t\sqrt{3}.
Из уравнения \frac{5}{2}t^{2}\sqrt{3}=\frac{35}{4}t\sqrt{3}
находим, что t=\frac{7}{2}
. Тогда BC=2t=7
, AC=5t=\frac{35}{2}
.
Пусть E
— проекция точки D
на прямую AC
. Поскольку BC\lt AC
, то \angle DAC=\angle BAC\lt90^{\circ}
, поэтому точка E
лежит на стороне AC
, а не на её продолжении. Тогда из прямоугольных треугольников CED
и AED
находим, что
DE=CD\sin30^{\circ}=\frac{1}{2}CD=\frac{5\sqrt{3}}{2},~CE=CD\cos30^{\circ}=5\sqrt{3}\cdot\frac{\sqrt{3}}{2}=\frac{15}{2},
AE=AC-CE=\frac{35}{2}-\frac{15}{2}=10,~\tg\angle DAE=\frac{DE}{AE}=\frac{\frac{5\sqrt{3}}{2}}{10}=\frac{\sqrt{3}}{4}.
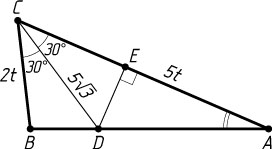
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1997 (июль), вариант 1, № 5
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.19, с. 40
