3951. Дан остроугольный треугольник ABC
. Окружность, проходящая через вершину B
и центр O
его описанной окружности, вторично пересекает стороны BC
и BA
в точках P
и Q
соответственно. Докажите, что точка пересечения высот треугольника POQ
лежит на прямой AC
.
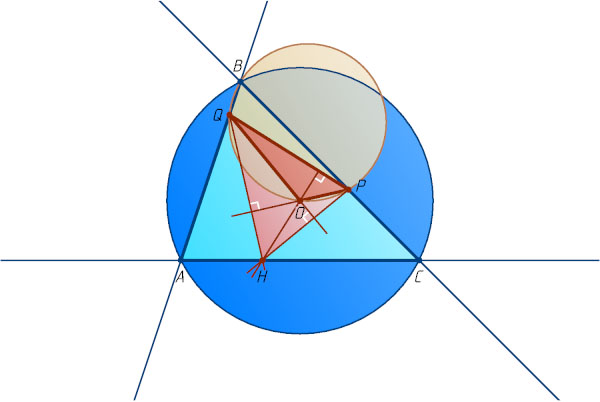
Указание. Пусть H
— точка пересечения с прямой AC
высоты OO_{1}
треугольника OPQ
. Тогда четырёхугольник OPCH
вписанный.
Решение. Обозначим \angle ABO=\angle BAO=\alpha
, \angle CBO=\angle BCO=\gamma
. Рассмотрим описанную окружность треугольника ABC
. Вписанный угол ACB
вдвое меньше центрального угла AOB
, поэтому
\angle ACB=\frac{1}{2}\angle AOB=\frac{1}{2}(180^{\circ}-2\alpha)=90^{\circ}-\alpha.
Рассмотрим описанную окружность четырёхугольника BPOQ
. Вписанные в неё углы OPQ
и OBQ
опираются на одну и ту же дугу, поэтому \angle OPQ=\angle OBQ=\alpha
. Аналогично \angle OQP=\angle OBP=\gamma
.
Пусть OO_{1}
— высота треугольника POQ
, а прямая OO_{1}
пересекается с прямой AC
в точке H
. Будем считать, что точка H
лежит на луче CA
. Угол POH
— внешний угол прямоугольного треугольника OO_{1}P
, поэтому
\angle POH=90^{\circ}+\angle OPQ=90^{\circ}+\alpha,
значит,
\angle POH+\angle PCH=(90^{\circ}+\alpha)+(90^{\circ}-\alpha)=180^{\circ}.
Следовательно, четырёхугольник OPCH
вписанный, и \angle OHP=\angle OCP=\gamma
.
Из прямоугольного треугольника HO_{1}P
находим, что
\angle HPO_{1}=90^{\circ}-\angle PHO_{1}=90^{\circ}-\gamma.
Пусть прямая QO
пересекается с прямой PH
в точке P_{1}
. Угол HP_{1}Q
— внешний угол треугольника PP_{1}Q
, поэтому
\angle HP_{1}Q=\angle P_{1}PQ+\angle PQP_{1}=\angle HPO_{1}+\angle OQP=(90^{\circ}-\gamma)+\gamma=90^{\circ}.
Следовательно, PP_{1}
— вторая высота треугольника OPQ
, а так как прямые OO_{1}
и PP_{1}
пересекаются в точке H
, то точка H
, лежащая на прямой AC
, — точка пересечения высот треугольника OPQ
. Что и требовалось доказать.
Автор: Емельянова Т. Л.
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2010-11, XXXVII, заключительный этап, 9 класс
Источник: Журнал «Квант». — 2011, № 5-6, с. 47
