3953. Периметр треугольника ABC
равен 4. На лучах AB
и AC
отмечены точки X
и Y
так, что AX=AY=1
. Отрезки BC
и XY
пересекаются в точке M
. Докажите, что периметр одного из треугольников ABM
и ACM
равен 2.
Указание. Рассмотрите вневписанную окружность треугольника ABC
, касающуюся стороны BC
.
Решение. Отрезки BC
и XY
пересекаются, поэтому точки B
и C
лежат по разные стороны от прямой XY
. Рассмотрим случай, когда AX\lt AB
и AY\gt AC
.
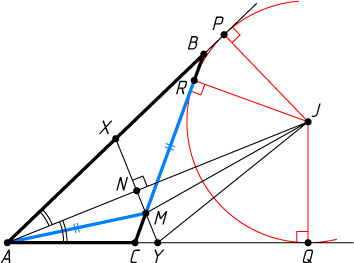
Пусть r
и J
— радиус и центр вневписанной окружности треугольника ABC
, касающейся стороны BC
в точке R
, а продолжений сторон AB
и AC
— в точках P
и Q
соответственно. Тогда AP=AQ=p=2
, где p=2
— полупериметр треугольника ABC
. Тогда AY=YQ=1
.
Поскольку эта окружность вписана в угол PAQ
, её центр лежит на биссектрисе угла, а так как треугольник XAY
равнобедренный, то точка N
пересечения AJ
и XY
— середина отрезка XY
.
Применяя теорему Пифагора к прямоугольным треугольникам MRJ
, MNJ
, YNJ
, YQJ
и YAN
, получим, что
MR^{2}=MJ^{2}-JR^{2}=(MN^{2}+NJ^{2})-r^{2}=MN^{2}+(YJ^{2}-YN^{2})-r^{2}=
=MN^{2}+(YQ^{2}+r^{2})-(AY^{2}-AN^{2})-r^{2}=MN^{2}+AN^{2}=AM^{2},
так как AY=YQ
. Значит, AM=MR
. Кроме того CR=CQ
как отрезки касательных, проведённых к окружности из одной точки.
Следовательно, периметр треугольника ACM
равен
AC+CM+AM=AC+CM+RM=AC+CR=AC+CQ=1+1=2.
Что и требовалось доказать. Если же AX\gt AB
и AY\lt AC
, то периметр треугольника AMB
равен 2.
Автор: Шмаров В. А.
Источник: Всероссийская олимпиада школьников. — 2010-11, XXXVII, заключительный этап, 10 класс
Источник: Журнал «Квант». — 2011, № 5-6, с. 47
