3954. На стороне BC
параллелограмма ABCD
(\angle A\lt90^{\circ}
) отмечена точка T
так, что треугольник ATD
— остроугольный. Пусть O_{1}
, O_{2}
и O_{3}
— центры описанных окружностей треугольников ABT
, DAT
и CDT
соответственно. Докажите, что точка пересечения высот треугольника O_{1}O_{2}O_{3}
лежит на прямой AD
.
Указание. Описанные окружности треугольников AO_{1}O_{2}
и DO_{2}O_{3}
симметричны описанной окружности четырёхугольника TO_{1}O_{2}O_{3}
относительно прямых O_{1}O_{2}
и O_{2}O_{3}
соответственно. Точка, симметричная ортоцентру треугольника относительно его стороны, лежит на описанной окружности треугольника.
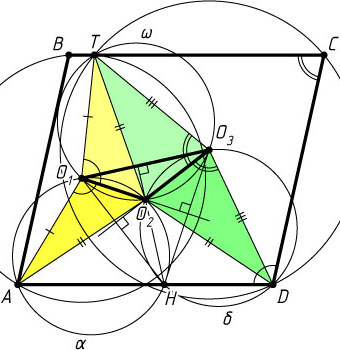
Решение. Прямая O_{1}O_{2}
— серединный перпендикуляр к общей стороне AT
треугольников ABT
и DAT
, поэтому \angle O_{1}AO_{2}=\angle O_{1}TO_{2}
. Аналогично \angle TO_{2}O_{2}=\angle DO_{3}O_{2}
. Обозначим \angle BAD=\varphi
.
Поскольку AO_{1}T
— центральные углы описанных окружностей треугольников ABT
и CDT
,
\angle AO_{1}T=360^{\circ}-2(180^{\circ}-\varphi)=2\varphi,~\angle TO_{1}O_{2}=\frac{1}{2}(360^{\circ}-2\varphi)=180^{\circ}-\varphi,
\angle TO_{3}O_{2}=\frac{1}{2}\angle DO_{3}T=\frac{1}{2}\cdot2\varphi=\varphi.
Поэтому \angle TO_{1}O_{2}+\angle TO_{3}O_{2}=180^{\circ}
. Значит, точки T
, O_{1}
, O_{2}
, O_{3}
лежат на одной окружности \omega
.
Треугольники AO_{1}O_{2}
и TO_{1}O_{2}
симметричны относительно прямой O_{1}O_{2}
, поэтому окружность \alpha
, описанная около треугольника AO_{1}O_{2}
, симметрична окружности \omega
, описанной около треугольника TO_{1}O_{2}
, относительно O_{1}O_{2}
. Аналогично окружность \delta
, описанная около треугольника DO_{2}O_{3}
, симметрична окружности \omega
относительно прямой O_{2}O_{3}
.
Пусть H
— точка пересечения высот треугольника O_{1}O_{2}O_{3}
. Поскольку \omega
— описанная окружность треугольника O_{1}O_{2}O_{3}
, точка, симметричная H
относительно прямой O_{1}O_{2}
, лежит на окружности \omega
, а так как окружность \alpha
симметрична окружности \omega
относительно O_{1}O_{2}
, то точка H
лежит на \alpha
. Аналогично докажем, что H
лежит на окружности \delta
. Таким образом, осталось доказать, что отличная от O_{2}
точка пересечения окружностей \alpha
и \delta
лежит на прямой AD
.
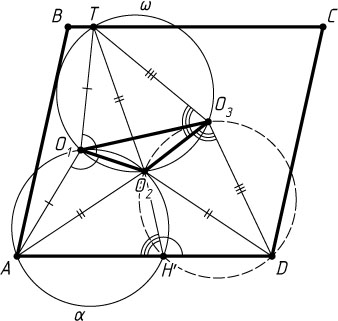
Пусть H'
— отличная от A
точка пересечения окружности \alpha
с прямой AD
. Четырёхугольники AO_{1}O_{2}H'
и TO_{1}O_{2}O_{3}
вписанные, поэтому
180^{\circ}-\angle DH'O_{2}=\angle AH'O_{2}=180^{\circ}-\angle AO_{1}O_{2}=180^{\circ}-\angle TO_{1}O_{2}=\angle TO_{3}O_{2}=\angle DO_{3}O_{2}.
Значит, четырёхугольник DO_{3}O_{2}H'
— также вписанный, точка H'
лежит на его описанной окружности \delta
, а поэтому совпадает с точкой H
— отличной от O_{2}
точкой пересечения окружностей \alpha
и \delta
. Отсюда следует доказываемое утверждение.
Автор: Емельянова Т. Л.
Источник: Всероссийская олимпиада школьников. — 2010-11, XXXVII, заключительный этап, 11 класс
Источник: Журнал «Квант». — 2011, № 5-6, с. 47

