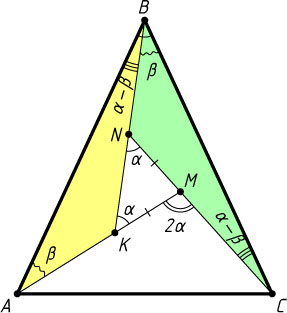
3955. Внутри равнобедренного треугольника ABC
(AB=BC
) выбрана точка M
таким образом, что \angle AMC=2\angle ABC
. На отрезке AM
нашлась такая точка K
, что \angle BKM=\angle ABC
. Докажите, что BK=KM+MC
.
Указание. Пусть N
— точка пересечения прямых CM
и BK
. Докажите равенство треугольников ABK
и BCN
.
Решение. Обозначим \angle BKM=\angle ABC=\alpha
. Тогда \angle AMC=2\alpha
.
Пусть N
— точка пересечения прямых CM
и BK
. По теореме о внешнем угле треугольника
\angle KNM=\angle AMC-\angle NKM=2\alpha-\alpha=\alpha=\angle MKN,
Значит, треугольник KMN
равнобедренный, KM=MN
. Следовательно, KM+MC=MN+MC=CN
.
Докажем равенство треугольников ABK
и BCN
. Обозначим \angle CBN=\beta
. Тогда \angle ABK=\alpha-\beta
, а по теореме о внешнем угле треугольника
\angle BCN=\angle KNM-\angle CBN=\alpha-\beta=\angle ABK,
\angle BAK=\angle BKM-\angle ABK=\alpha-(\alpha-\beta)=\beta=\angle CBN,
Кроме того, по условию задачи AB=BC
, значит, треугольники ABK
и BCN
равны по стороне и двум прилежащим к ней углам. Поэтому BK=CN
. Следовательно,
KM+MC=MN+MC=CN=BK.
Что и требовалось доказать.
Автор: Берлов С. Л.
Источник: Всероссийская олимпиада школьников. — 2006-07, XXXIII, окружной этап, 8 класс
Источник: Журнал «Квант». — 2007, № 5, с. 48
