3957. В треугольнике ABC
проведена биссектриса BB_{1}
. Перпендикуляр из B_{1}
на BC
пересекает дугу BC
описанной окружности треугольника ABC
в точке K
. Перпендикуляр из точки B
на AK
пересекает AC
в точке L
. Докажите, что точки K
, L
и середина дуги AC
(не содержащей точку B
) лежат на одной прямой.
Указание. Точки B
, K
, L
и B_{1}
лежат на одной окружности.
Решение. Пусть продолжение биссектрисы BB_{1}
пересекает описанную окружность треугольника ABC
в точке M
. Тогда M
— середина дуги AC
, не содержащей точку B
. Достаточно доказать, что луч KL
— биссектриса угла AKC
(тогда луч KL
также проходит через точку M
).
Обозначим \angle KAC=\alpha
. Вписанные углы KBC
и KAC
опираются на одну и ту же дугу, поэтому \angle KBC=\angle KAC=\alpha
.
Пусть прямые AK
и BL
пересекаются в точке T
, а прямые KB_{1}
и BC
— в точке S
. Из прямоугольных треугольников ATL
и BSK
находим, что
\angle BLB_{1}=\angle TLA=90^{\circ}-\alpha,~\angle BKB_{1}=\angle BKS=90^{\circ}-\alpha.
Из точек L
и K
, лежащих по одну сторону от прямой BB_{1}
, отрезок BB_{1}
виден под одним и тем же углом, значит, точки B
, K
, L
и B_{1}
лежат на одной окружности. Вписанные в эту окружность углы BB_{1}K
и BLK
опираются на одну и ту же дугу, поэтому \angle BB_{1}K=\angle BLK
. Значит, равны и дополняющие их до 90^{\circ}
углы CBB_{1}
и AKL
, а так как \angle CBB_{1}=\frac{1}{2}\angle ABC
и \angle AKC=\angle ABC
, то \angle AKL=\frac{1}{2}\angle AKC
, т. е. KL
— биссектриса угла AKC
. Следовательно, луч KL
проходит через середину M
дуги AC
, не содержащей точку A
. Что и требовалось доказать.
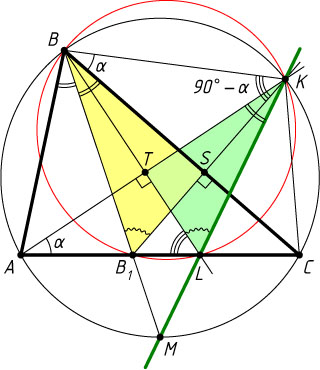
Автор: Астахов В. В.
Источник: Всероссийская олимпиада школьников. — 2006-07, XXXIII, заключительный этап, 9 класс
Источник: Журнал «Квант». — 2007, № 5, с. 50, задача 6, 9 класс
