3969. На стороне AB
треугольника ABC
со сторонами BC=a
, AC=b
, AB=c
и площадью S
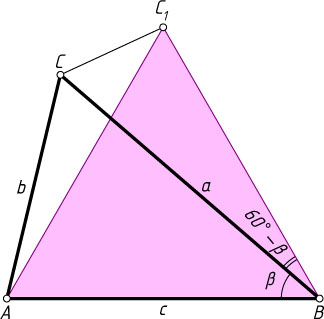
в одной полуплоскости с ним построен правильный треугольник ABC_{1}
. Докажите, что
CC_{1}^{2}=\frac{1}{2}(a^{2}+b^{2}+c^{2})-2S\sqrt{3}.
Указание. Примените теорему косинусов.
Решение. Обозначим \angle ABC=\beta
. Пусть луч BC
проходит между сторонами угла ABC_{1}
. Тогда \angle CBC_{1}=60^{\circ}-\beta
. Из треугольников ABC
и CBC_{1}
по теореме косинусов находим, что
\cos\beta=\frac{a^{2}+c^{2}-b^{2}}{2ac},
CC_{1}^{2}=a^{2}+c^{2}-2ac\cos(60^{\circ}-\beta)=a^{2}+c^{2}-2ac\left(\frac{1}{2}\cos\beta+\frac{\sqrt{3}}{2}\sin\beta\right)=
=a^{2}+c^{2}-2ac\left(\frac{1}{2}\cdot\frac{a^{2}+c^{2}-b^{2}}{2ac}+\frac{\sqrt{3}}{2}\sin\beta\right)=
=a^{2}+c^{2}-\left(\frac{1}{2}(a^{2}+c^{2}-b^{2})+\sqrt{3}ac\sin\beta\right)=\frac{1}{2}(a^{2}+b^{2}+c^{2})-2S\sqrt{3}.
Что и требовалось доказать.
Аналогично для любого другого расположения точки C_{1}
.
Примечание. Из доказанного равенства следует, что
a^{2}+b^{2}+c^{2}\geqslant4S\sqrt{3},
причём равенство достигается тогда и только тогда, когда треугольник равносторонний (точка C_{1}
совпадает с C
).
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 3.22, с. 33
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 208, с. 34
