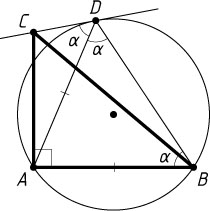
3994. Окружность радиуса 3 проходит через вершины A
и B
прямоугольного треугольника ABC
с катетом AB=5
. Прямая CD
касается этой окружности в точке D
. Найдите величину угла ABD
и длину второго катета AC
, если луч DA
делит угол CDB
пополам.
Ответ. \arcsin\frac{5}{6}
, \frac{225}{16\sqrt{11}}
.
Указание. Примените теорему об угле между касательной и хордой и теорему синусов.
Решение. Обозначим \angle ADC=\angle ADB=\alpha
. Из теоремы об угле между касательной и хордой следует, что
\angle ABD=\angle ADC=\angle ADB=\alpha.
Значит, треугольник ABD
— равнобедренный. Поэтому \alpha\lt90^{\circ}
. Следовательно, точка D
лежит на большей дуге AB
.
Поскольку R=3
— радиус окружности, описанной около треугольника ADB
, то
\sin\angle ADB=\sin\alpha=\frac{AB}{2R}=\frac{5}{6}.
Следовательно, \angle ABD=\arcsin\frac{5}{6}
. Кроме того, \sin\alpha=\frac{5}{6}\gt\frac{1}{\sqrt{2}}
, поэтому \alpha\gt45^{\circ}
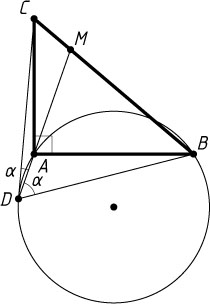
. Докажем, что точка D
лежит внутри угла BAC
. Предположим, что это не так (рис. 2). Пусть луч DA
пересекает отрезок BC
в точке M
. Тогда
90^{\circ}=\angle CAB=\angle CAM+\angle BAM\gt\angle CDA+\angle BDA=\alpha+\alpha\gt90^{\circ},
что невозможно. Следовательно, точка D
лежит внутри угла BAC
(рис. 1).
Поскольку
\angle CAD=\angle CAB-\angle DAB=90^{\circ}-(180^{\circ}-2\alpha)=2\alpha-90^{\circ},
то
\sin\angle ACD=\sin(180^{\circ}-(\angle CAD+\angle ADC))=\sin(\angle CAD+\angle ADC)=
=\sin(2\alpha-90^{\circ}+\alpha)=\sin(3\alpha-90^{\circ})=-\cos3\alpha.
По теореме синусов из треугольника ACD
находим, что
AC=AD\cdot\frac{\sin\angle ADC}{\sin\angle ACD}=5\cdot\frac{\sin\alpha}{-\cos3\alpha}=
=\frac{5\sin\alpha}{\cos\alpha(4\sin^{2}\alpha-1)}=\frac{5\cdot\frac{5}{6}}{\sqrt{1-\left(\frac{5}{6}\right)^{2}}\cdot\left(4\cdot\frac{25}{36}-1\right)}=\frac{225}{16\sqrt{11}}.
Источник: Вступительный экзамен на факультет психологии МГУ. — 2004, вариант 1, № 4
Источник: Вступительные экзамены и олимпиады по математике 2003—2005 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2006. — с. 164

