4013. Основание равнобедренного треугольника равно 4\sqrt{2}
, а медиана, проведённая к боковой стороне, равна 5. Найдите боковые стороны.
Ответ. 6.
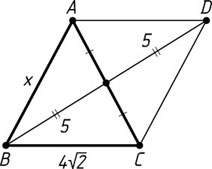
Указание. Достройте данный треугольник до параллелограмма.
Решение. Обозначим через x
боковую сторону AB
равнобедренного треугольника ABC
(BC=4\sqrt{2}
). На продолжении медианы BM
за точку M
отложим отрезок DM
, равный BM
. Тогда BADC
— параллелограмм. Поэтому
AC^{2}+BD^{2}=2(AB^{2}+BC^{2}),~\mbox{или}~x^{2}+10^{2}=2(4\sqrt{2})^{2}+2x^{2}.
Отсюда находим, что x^{2}=36
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.011, с. 159
Источник: Вступительный экзамен в МАТИ. — 1977
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 2.7, с. 17
