4016. В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20. Найдите биссектрису угла при основании треугольника.
Ответ. 6.
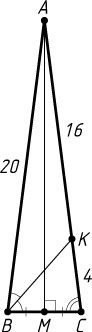
Указание. Пусть BK
— биссектриса угла при основании BC
равнобедренного треугольника ABC
. Примените теорему косинусов к треугольнику BKC
.
Решение. Пусть BK
— биссектриса угла при основании BC
равнобедренного треугольника ABC
(AB=AC=20
, BC=5
), M
— середина BC
.
Из прямоугольного треугольника AMC
находим, что
\cos\angle C=\frac{MC}{AC}=\frac{1}{8}.
По свойству биссектрисы треугольника
\frac{AK}{KC}=\frac{AB}{BC}=\frac{4}{1}.
Поэтому KC=\frac{1}{5}AC=4
. По теореме косинусов из треугольника BKC
находим, что
BK^{2}=BC^{2}+KC^{2}-2BC\cdot KC\cos\angle C=25+16-2\cdot5\cdot4\cdot\frac{1}{8}=36.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.077, с. 64
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.15, с. 40
