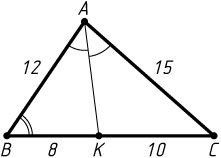
4019. Вычислите биссектрису треугольника ABC
, проведённую из вершины A
, если BC=18
, AC=15
, AB=12
.
Ответ. 10.
Указание. Примените теорему косинусов.
Решение. Первый способ. Пусть AK
— биссектриса треугольника ABC
. Тогда
\frac{CK}{KB}=\frac{AC}{AB}=\frac{15}{12}=\frac{5}{4}.
Поэтому
BK=\frac{4}{9}BC=\frac{4}{9}\cdot18=8.
По теореме косинусов из треугольника ABC
находим, что
\cos\angle B=\frac{AB^{2}+BC^{2}-CA^{2}}{2AB\cdot BC}=\frac{144+324-225}{2\cdot12\cdot18}=\frac{9}{16}.
Следовательно,
AK^{2}=BK^{2}+AB^{2}-2BK\cdot AB\cos\angle B=144+64-108=100.
Второй способ. Пусть AK
— биссектриса треугольника ABC
. Тогда
\frac{CK}{KB}=\frac{AC}{AB}=\frac{15}{12}=\frac{5}{4}.
Поэтому
BK=\frac{4}{9}BC=\frac{4}{9}\cdot18=8,~CK=\frac{5}{9}BC=\frac{5}{9}\cdot18=10.
По формуле для квадрата биссектрисы треугольника (см. задачу 791) находим, что
AK^{2}=AB\cdot AC-BK\cdot CK=12\cdot15-8\cdot10=180-80=100.
Следовательно, AK=10
.
