4021. Докажите, что если a
и b
— две стороны треугольника, \gamma
— угол между ними и l
— биссектриса этого угла, то
l=\frac{2ab\cos\frac{\gamma}{2}}{a+b}.
Указание. Сложите площади треугольников, на которые биссектриса разбивает данный треугольник.
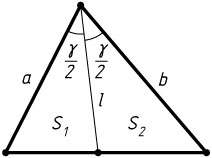
Решение. Пусть S
— площадь данного треугольника, S_{1}
и S_{2}
— площади треугольников, на которые указанная биссектриса разбивает данный треугольник. Тогда S=S_{1}+S_{2}
, или
\frac{1}{2}ab\sin\gamma=\frac{1}{2}al\sin\frac{\gamma}{2}+\frac{1}{2}bl\sin\frac{\gamma}{2},~\mbox{или}
ab\sin\frac{\gamma}{2}\cos\frac{\gamma}{2}=\frac{1}{2}(a+b)l\sin\frac{\gamma}{2}.
Поскольку \sin\frac{\gamma}{2}\ne0
, то l=\frac{2ab\cos\frac{\gamma}{2}}{a+b}
.
Примечание. Пусть l_{c}=CQ
— биссектриса внешнего угла при вершине C
треугольника ABC
(AC\ne BC
, Q
— точка на прямой AB
). Тогда
l_{c}=\frac{2ab\sin\frac{\gamma}{2}}{|a-b|}.
Действительно, если a\gt b
, а CL
— биссектриса треугольника ABC
, то \angle LCQ=90^{\circ}
, поэтому
\angle BCQ=90^{\circ}+\frac{\gamma}{2},~\angle ACQ=90^{\circ}-\frac{\gamma}{2}.
Значит,
S_{\triangle ABC}=S_{\triangle BCQ}-S_{\triangle ACQ},
или
\frac{1}{2}ab\sin\alpha=\frac{1}{2}l_{c}a\sin\left(90^{\circ}+\frac{\gamma}{2}\right)-\frac{1}{2}l_{c}b\sin\left(90^{\circ}-\frac{\gamma}{2}\right),
ab\sin\alpha=l_{c}a\sin\left(90^{\circ}+\frac{\gamma}{2}\right)-l_{c}b\sin\left(90^{\circ}-\frac{\gamma}{2}\right),
2ab\sin\frac{\alpha}{2}\cos\frac{\gamma}{2}=l_{c}a\cos\frac{\gamma}{2}-l_{c}b\cos\frac{\gamma}{2},
откуда
l_{c}=\frac{2ab\sin\frac{\gamma}{2}}{a-b}.
Если a\lt b
, то аналогично получим, что
l_{c}=\frac{2ab\sin\frac{\gamma}{2}}{b-a}.
Источник: Вступительный экзамен в МФТИ. — 1962, билет 9, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 62-9-4, с. 94
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 192, с. 33, № 427, с. 67
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — с. 268
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 17
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 17, с. 6
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 37
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 30
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 27, с. 99
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.48, с. 87, № 12.37(б), с. 292; № 12.88, с. 297
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 4.47, с. 88; № 12.83, с. 308
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 587
