4035. В равнобедренной трапеции даны основания a=21
, b=9
и высота h=8
. Найдите радиус описанной окружности.
Ответ. \frac{85}{8}
.
Указание. Окружность, описанная около трапеции ABCD
, описана и около треугольника ACD
.
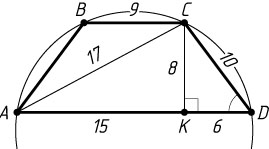
Решение. Из вершины C
меньшего основания BC
трапеции ABCD
опустим перпендикуляр CK
на большее основание AD
. Тогда CK=8
. Если AD=21
, BC=9
, то
KD=\frac{AD-BC}{2}=6,~CD=\sqrt{CK^{2}+DK^{2}}=\sqrt{8^{2}+6^{2}}=10,
\sin\angle D=\frac{CK}{CD}=\frac{4}{5},~AC=\sqrt{AK^{2}+CK^{2}}=\sqrt{15^{2}+8^{2}}=17.
Если R
— радиус окружности, описанной около трапеции ABCD
, то
R=\frac{AC}{2\sin\angle D}=\frac{85}{8}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.003, с. 159
Источник: Вступительный экзамен на технологический факультет МИСиС. — 1982, № 5
Источник: Журнал «Квант». — 1983, № 5, с. 58
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.10, с. 86
