4040. В трапеции ABCD
точка K
— середина основания AB
, M
— середина основания CD
. Найдите площадь трапеции, если известно, что DK
— биссектриса угла D
, BM
— биссектриса угла B
, наибольший из углов при нижнем основании равен 60^{\circ}
, а периметр равен 30.
Ответ. 15\sqrt{3}
.
Указание. Через вершину меньшего основания проведите прямую, параллельную боковой стороне трапеции, и примените теорему косинусов.
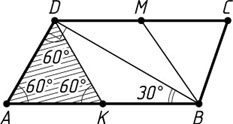
Решение. Пусть K
— середина большего основания AB
трапеции ABCD
. Предположим, что \angle DAB=60^{\circ}
(рис. 1). Поскольку
\angle ADK=\angle KDC=\angle AKD,
то треугольник ADK
— равносторонний, DK=AK=KB
. Поэтому \angle ADB=90^{\circ}
, а \angle DBA=30^{\circ}
. Но
\angle DBA\lt\angle MBA=\frac{1}{2}\angle ABC.
Поэтому \angle ABC\gt60^{\circ}
, что невозможно. Следовательно, \angle ABC=60^{\circ}
(рис. 2).
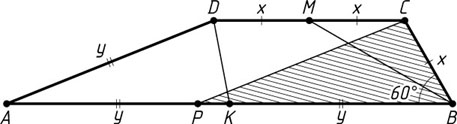
Обозначим BC=MC=MD=x
, AD=AK=KB=y
. Тогда x+y=10
. Проведём через вершину C
прямую, параллельную AD
, до пересечения с основанием AB
в точке P
. В треугольнике BCP
известно, что
BC=x,~CP=AD=y,~BP=AB-AP=AB-DC=2(y-x),~\angle CBP=60^{\circ}.
По теореме косинусов
y^{2}=x^{2}+4(y-x)^{2}-2x(y-x).
Из полученной системы
\syst{x+y=10\\y^{2}=x^{2}+4(y-x)^{2}-2x(y-x)\\}
находим, что x=3
, y=7
. Тогда высота трапеции равна x\sin60^{\circ}=\frac{3\sqrt{3}}{2}
. Следовательно,
S_{ABCD}=(x+y)\cdot\frac{3\sqrt{3}}{2}=15\sqrt{3}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1973, вариант 4, № 2
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 269
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.23, с. 12

