4043. В треугольнике ABC
точка D
делит сторону AB
пополам, а точка E
лежит на стороне BC
, причём отрезок BE
в 3 раза меньше стороны BC
. Отрезки AE
и CD
пересекаются в точке O
. Найдите AB
, если известно, что AE=5
, OC=4
, а угол AOC
равен 120^{\circ}
.
Ответ. 2\sqrt{7}
.
Указание. Продолжите отрезок AE
до пересечения с прямой, проведённой через вершину C
параллельно AB
, и рассмотрите две пары образовавшихся подобных треугольников.
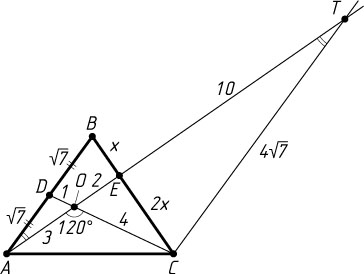
Решение. Проведём через точку C
прямую, параллельную AB
, и продолжим отрезок AE
до пересечения с проведённой прямой в точке T
. Из подобия треугольников CET
и BEA
следует, что
CT=2AB=4AD.
Из подобия треугольников COT
и DOA
находим, что
\frac{CO}{OD}=\frac{TO}{OA}=\frac{CT}{AD}=4.
Поэтому
OD=\frac{1}{4}CO=1,~AO=\frac{1}{5}AT=\frac{1}{5}(AE+ET)=
=\frac{1}{5}(AE+2AE)=3\cdot\frac{1}{5}AE=3.
По теореме косинусов из треугольника AOD
находим, что
AD^{2}=AO^{2}+DO^{2}-2AO\cdot DO\cos\angle AOD=9+1-2\cdot3\cdot1\cdot\cos60^{\circ}=7.
Следовательно, AB=2AD=2\sqrt{7}
.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1986, вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 87
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 6.32, с. 59
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.33.1, с. 62
