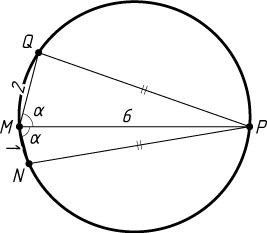
4045. Из точки M
на окружности проведены три хорды: MN=1
, MP=6
, MQ=2
. При этом углы NMP
и PMQ
равны. Найдите радиус окружности.
Ответ. 2\sqrt{\frac{34}{15}}
.
Указание. Выразите отрезки NP
и PQ
по теореме косинусов из треугольников NMP
и PNQ
.
Решение. Обозначим \angle NMP=\angle PMQ=\alpha
. Выразим равные отрезки NP
и PQ
по теореме косинусов из треугольников NMP
и PMQ
соответственно:
NP^{2}=MN^{2}+MP^{2}-2NM\cdot MP\cos\alpha,
PQ^{2}=MP^{2}+MQ^{2}-2MP\cdot MQ\cos\alpha.
Приравняв правые части полученных равенств, получим уравнение, из которого найдём, что \cos\alpha=\frac{1}{4}
. Тогда
\sin\alpha=\frac{\sqrt{15}}{4}.
Если R
— искомый радиус, то
R=\frac{NP}{2\sin\alpha}=\frac{\sqrt{34}}{\frac{\sqrt{15}}{2}}=2\sqrt{\frac{34}{15}}.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1990, № 4
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.19, с. 87
