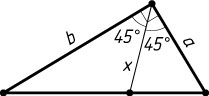
4051. Катеты прямоугольного треугольника равны a
и b
. Найдите биссектрису, проведённую из вершины прямого угла.
Ответ. \frac{ab\sqrt{2}}{a+b}
.
Указание. Примените формулу площади треугольника.
Решение. Пусть x
— искомая биссектриса. Сумма площадей треугольников, на которые биссектриса разбивает данный треугольник, равна площади данного треугольника, т. е.
\frac{1}{2}ax\sin45^{\circ}+\frac{1}{2}bx\sin45^{\circ}=\frac{ab}{2}.
Отсюда находим, что x=\frac{ab\sqrt{2}}{a+b}
.
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 19, с. 169
Источник: Задачи по математике и физике, дававшиеся на приёмных испытаниях в 1947—1953 гг. — М.: МФТИ, 1956. — № 45, с. 38
Источник: Вступительный экзамен в МФТИ. — 1960, билет 1, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 60-1-1, с. 77
Источник: Вступительный экзамен в МИЭТ. — 1977
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 8, с. 185
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.6, с. 39
Источник: Пособие по математике для поступающих в вузы / Под ред. Г. Н. Яковлева. — 3-е изд. — М.: Наука, 1988. — № 40, с. 31
