4054. Площадь треугольника ABC
равна S
. Углы CAB
, ABC
и ACB
равны \alpha
, \beta
и \gamma
соответственно. Найдите высоты треугольника.
Ответ. \frac{\sqrt{2S\sin\alpha\sin\beta\sin\gamma}}{\sin\alpha}
; \frac{\sqrt{2S\sin\alpha\sin\beta\sin\gamma}}{\sin\beta}
; \frac{\sqrt{2S\sin\alpha\sin\beta\sin\gamma}}{\sin\gamma}
.
Указание. Выразите высоту, проведённую к стороне BC
через AB
и AC
.
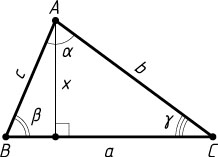
Решение. Обозначим BC=a
, AC=b
, AB=c
. Пусть высоты, опущенные на эти стороны, равны x
, y
и z
соответственно. Тогда
b=\frac{x}{\sin\beta},~c=\frac{x}{\sin\gamma},~S=\frac{1}{2}bc\sin\alpha=\frac{\frac{1}{2}x^{2}\sin\alpha}{\sin\beta\sin\gamma}.
Отсюда находим, что
x^{2}=\frac{2S\sin\beta\sin\gamma}{\sin\alpha}.
Следовательно,
x=\frac{\sqrt{2S\sin\alpha\sin\beta\sin\gamma}}{\sin\alpha}.
Аналогично найдём y
и z
.
Источник: Вступительный экзамен на химический факультет МГУ. — 1979, вариант 3, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 56
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.9, с. 39
