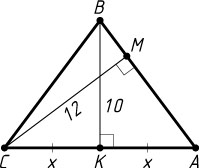
4061. Найдите площадь равнобедренного треугольника, если высота, опущенная на основание, равна 10, а высота, опущенная на боковую сторону, равна 12.
Ответ. 75.
Указание. Составьте уравнение относительно половины основания треугольника.
Решение. Пусть BK
и CM
— высоты равнобедренного треугольника ABC
(AB=BC
, BK=10
, CM=12
). Обозначим AK=KC=x
. Тогда
AB^{2}=BK^{2}+AK^{2}=100+x^{2},
S_{\triangle ABC}=\frac{1}{2}AC\cdot BK=\frac{1}{2}AB\cdot CM.
Поэтому
AC\cdot BK=AB\cdot CM,~\mbox{или}~2x\cdot10=\sqrt{100+x^{2}}\cdot12.
Из этого уравнения находим, что x=\frac{15}{2}
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}AC\cdot BK=75.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1979 (отделение политической экономии), вариант 2, № 2C
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 99
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 49, с. 196
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.12, с. 39
