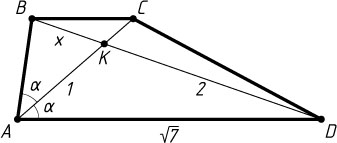
4068. В трапеции ABCD
основание AD
равно \sqrt{7}
. Диагонали AC
и DB
пересекаются в точке K
. Известно, что AK=1
, KD=2
, \angle BAC=\angle DAC
. Найдите площадь треугольника ABC
.
Ответ. \frac{2\sqrt{3}}{9}
.
Указание. Найдите \angle CAD
по теореме косинусов из треугольника KAD
и воспользуйтесь свойством биссектрисы треугольника.
Решение. Обозначим \angle CAD=\angle BAC=\alpha
, BK=x
. По теореме косинусов из треугольника AKD
находим, что
\cos\alpha=\frac{AD^{2}+AK^{2}-KD^{2}}{2AK\cdot AD}=\frac{2}{\sqrt{7}}.
Тогда
\sin\alpha=\frac{\sqrt{3}}{\sqrt{7}},~\cos2\alpha=\cos^{2}\alpha-\sin^{2}\alpha=\frac{1}{7}.
По свойству биссектрисы из треугольника ABD
находим, что \frac{AB}{BK}=\frac{AD}{DK}
. Поэтому
AB=\frac{AD\cdot BK}{DK}=\frac{x\sqrt{7}}{2}.
По теореме косинусов
BD^{2}=AB^{2}+AD^{2}-2AB\cdot AD\cos2\alpha,
или
(x+2)^{2}=\left(\frac{x\sqrt{7}}{2}\right)^{2}+(\sqrt{7})^{2}-2\cdot\frac{x\sqrt{7}}{2}\cdot\sqrt{7}\cdot\frac{1}{7}.
Из этого уравнения находим, что x=\frac{2}{3}
или x=6
. Второе решение не удовлетворяет условию задачи, так как в этом случае BK+AK\lt AB
(7\lt3\sqrt{7})
.
Поскольку
\angle BCA=\angle CAD=\angle BAC=\alpha,
то треугольник ABC
— равнобедренный, BC=AB=\frac{\sqrt{7}}{3}
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB^{2}\sin\angle ABC=\frac{1}{2}AB^{2}\sin2\alpha=\frac{2\sqrt{3}}{9}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1983, вариант 3, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 66
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 8, с. 139
