4078. В треугольнике ABC
отношение стороны BC
к стороне AC
равно 3, а \angle ACB=\alpha
. Из вершины C
проведены два луча, делящие угол ACB
на три равные части. Найдите отношение отрезков этих лучей, заключённых внутри треугольника ABC
.
Ответ. \frac{2\cos\frac{\alpha}{3}+3}{6\cos\frac{\alpha}{3}+1}
.
Указание. Если a
и b
— стороны треугольника, а \alpha
— угол между ними, то биссектрису l
этого угла можно вычислить по формуле
l=\frac{2ab\cos\frac{\alpha}{2}}{a+b}.
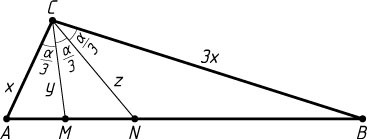
Решение. Пусть M
и N
— точки пересечения указанных лучей со стороной AB
(M
— между A
и N
). Обозначим AC=x
, CM=y
, CN=z
. Тогда BC=3x
.
S_{\triangle ACN}=\frac{1}{2}xz\sin\frac{2\alpha}{3}=S_{\triangle ACM}+S_{\triangle MCN}=\frac{1}{2}xy\sin\frac{\alpha}{3}+\frac{1}{2}yz\sin\frac{\alpha}{3}.
Отсюда находим, что y=\frac{2xz\cos\frac{\alpha}{3}}{x+z}
. Из треугольника MCB
аналогично находим, что
z=\frac{6xy\cos\frac{\alpha}{3}}{y+3x}.
Выразим x
из полученных равенств:
x=\frac{yz}{2z\cos\frac{\alpha}{3}-y},~x=\frac{yz}{6y\cos\frac{\alpha}{3}-3z}.
Приравняв правые части этих выражений, получим уравнение
2z\cos\frac{\alpha}{3}-y=6y\cos\frac{\alpha}{3}-3z.
Разделим обе части этого уравнения на z
и найдём нужное отношение \frac{y}{z}
:
\frac{y}{z}=\frac{2\cos\frac{\alpha}{3}+3}{6\cos\frac{\alpha}{3}+1}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1969, № 4, вариант 5
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 118, с. 16
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 118, с. 15
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.23, с. 40
